Christian Lange | Juni 2002 |
The golden angle
Observing the nature we recognize its inner harmony everywhere. This harmony we meet even in music.
If we take the half lenght of a chord double frequence, if we take a third of the chord, we get the triple frequence ecc.. In this way we get the acustic –law where l is the lenght of the chord and f the frequence:
l * f = 1
l | f |
1 | 1 |
1/2 | 2 |
1/3 | 3 |
... | ... |
1/n | n |
Mathematically this is the hyperbolic Y=1/X with his grafic rapresentation :

Walter Schauberger , based on the acustic law, discovered the hyperbolic cone. This is the hyperbolic function rotated around the Y-axis rapresenting the three dimensional acustic law.

On this hyperbolic cone you can create a hyperbolic spiral when the rate of curvature and climbing are equal.
Looking from the top of the spiral downwards you get this figure, which is the same of a water vortex or a spiral galaxy:
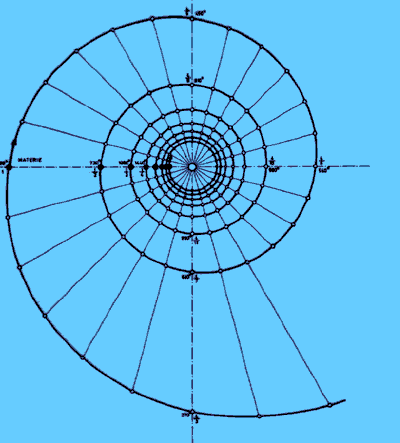


If we cut the hyperbolic cone with a plane on different highs Z0 in combination with different cutting angles
α we obtain all possible egg-curves with different size and shape (big, small, long or short).

The german astronomic researcher Johannes Kepler discovered the 3 famous law’s describing planets movements around the sun studying the harmony in acustics. In his opera Astronomia nova – physica coelestis – de motibus stellae MARTIS from the year 1609 Kepler wrote: "The trajectory of a planet is not a circle but it has the shape of an egg." and "we can show, that the trajectory is really an egg-curve and not elliptical". This means that the hyperbolic cone or the three dimensional acustic law contains the laws of planets movements and he represent an universal law od nature. Kepler used the elliptic equations only for semplifying the calculations obtaining an approximation telling everybody that in reality planets are following egg-curves. Today most scientist think, that planets move on elliptic curves even if its well know, that the gravitational potential of the sun is hyperbolic.
Besides the acustic law, there’s another universal law that itself is manifested in the music notes too: The golden section.
The harmonic proportions in music goes with the Fibonacci-series (1, 1, 2, 3, 5, 8, 13, 21, 34, ...), where every number is the sum of the two numbers before in the series. Dividing a number by its number before, we obtain the irrational number of the golden section increase in precision using higher numbers: Phi
ф = 1,618034...The number
ф (=1,618...) is the only one for which we can affirm:
1,618 = 1/0,618 = 1,618 – 1 and
1,6182 = 2,618 and
0,618 ~ (
π / 4)2
Another representation of Phi is an infinite fraction based esclusively on the number 1.

If the hyperbolic cones and the golden section represent universal laws of nature, may-be they is a relationship between them ? Yes there is a common base and we will demonstrate it.
For this purpose we have to cut the hyperbolic cone in a way, that we obtain an egg with a golden section i.e. that is 1,618034 times longer than width. For the calculation of the egg-coordinates we use the parametric equation of Prof. Norbert Harthun and Prof. Ines Rennert:

By an iteration method we can find out, that only the cutting angle of 51,84° and high Z0 = 7,65 is good to get the egg with golden proportions. Varying the cutting angle or high, the value diverge fastly from
ф=1,618034... . The golden egg has a lenght of 0,423584 units and a width of 0,261789 units, the volume is 0,009408 volume-units.

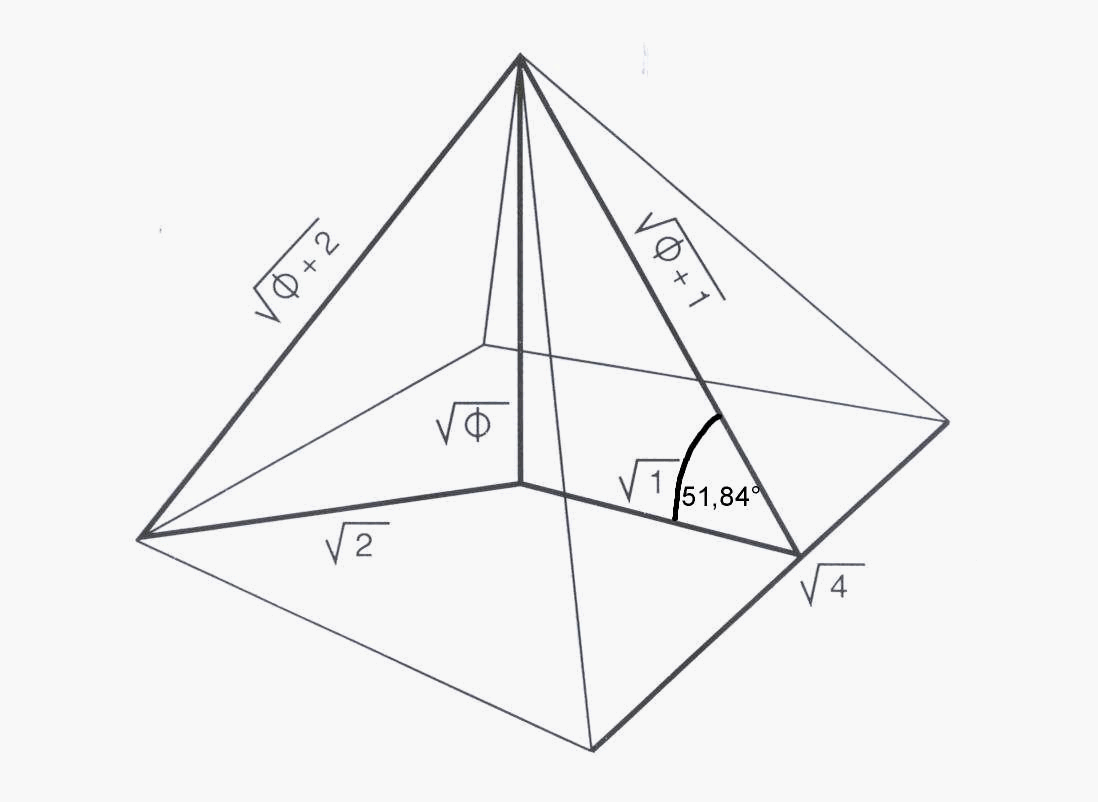
We were searching for the relationship between the hyperbolic law and the golden section. For this purpose we will study the geometry of the Cheops-Pyramide. If we divide the lenght of the 4 borders around the quadratic base by
π, we get the high of this pyramid. The angle between the side-triangles and the base is 51,84°. If you draw a line between pyramids top to the mid of one of the 4 borders, the lenght of this line is 1,618034 times longer than the line from the center of the quadratic base to the mid of a side borderline. this means that the hyperbolic cone give us the golden section using the pyramid angle of 51,84° for the inclination of the cutting plane. For this reason, the angle of 51,84° is the golden angle.
Another analogy come from the water molecole examinated intensively by Viktor and Walter Schauberger. The shape of the water-molecole is V-like and symmetric. The angle between the two hydrogen-atoms is ca. 104°, this means ca. 52° from middle-axis, very close to the golden angle. Viktor Schauberger said, that the energy of a single water-drop is equal to the power output of an average electrical-power station. In addition to this he said, that we have to understand copy nature for getting this natural energy for free. Nature is telling us its secret by harmonic laws (hyperbolic cone, golden section). I think, that Neutrinopower, Chi, Prana, live-force, Orgone-Energy, time-emanation, nervous ether, gravitation ecc. have the same origin like the pyramid-energy that manifest the same universal law like the planets that are following egg-curves on the hyperbolic cone which is the law of music. Somebody said, that the universe is singing.
Dipl. Ing. Christian Lange
Via Ciro Menotti, 13
70029 Santeramo in Colle (BA) - Italy
e-mail:christian.lange2@tin.it
Thanks to: Jörg Schauberger, Prof. Norbert Harthun, Prof. Ines Rennert, Claus Radlberger, Klaus Rauber
and my friend Arturo Rinaldi, that gave me the idea to calculate an egg with the golden section.
Sources: www.pks.or.at, „The hyperbolic cone" from Claus Radlberger (in german)